Find the area between the graph of f of x equals the product of x and e raised to negative 1 times x squared power and the x-axis for the interval (0, ∞). Your work must include the proper notation...

Question

Find the area between the graph of 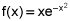 and the x-axis for the interval (0, ∞). Your work must include the proper notation and show the antiderivative. If the integral diverges, show why.

Answer 1

Area, A = ∫₀^∞xe^{-x^2}dx

Let u = x², du = 2xdx

When x = ∞, u = ∞

When x = 0, u = 0

A = (1/2)∫₀^∞e^-udu = (1/2)[-e^u]₀^∞

= (1/2) [-lim e^-n + e⁰]

n→∞

= (1/2)(-0 +1) = 1/2

Answer 2

We start by evaluating the antiderivative of the given function which is -(1/2)e^{-x^2}

We now must evaluate the antiderivative as x tends to infinity and evaluate the antiderivative at x=0.

If x tends to infinity, the antiderivative will be zero, while in the second case the antiderivative will be equal to (-1/2)e⁰=-1/2. The integral is therefore given by the difference between these two terms 0-(-1/2)=1/2

The integral does not diverge since the term e^(-x^2) tends to zero very quickly.

Best,

Davide