
Bradford T. answered • 02/16/21
Retired Engineer / Upper level math instructor
From description, P(0) = 100
P' = 0.08P(1-P/1000)
We can solve the differential equation by separating the variables
1000∫dP/(P(1000-P) = 0.08/1000 ∫dt = 0.08t +C
Concentrating on the left hand side of the equation
1000/(P(1000-P) = A/P + B/(1000-P) --> A = B = 1
1000∫1/P + 1/(1000-P) dP = 1000(ln(P) - ln(P-1000)) = 1000ln(P/(P-1000))
Putting left and right sides together
ln(P/(P-1000)) = 0.08t + C
When t = 0
C = ln(-100/(900)) = ln(-1/9)
Taking both sides to power of e
P/(P-1000) = e0.08t + ln(-1/9) = -e0.08t/9
e0.08t=9P/(1000-P)
When P = 900
e0.08t= 9(900/900)
0.08t = ln(9)
t = ln(9)/0.08 ≈ 28 months ≈ 2.3 years


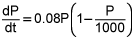 , where P t is measured in months. When does the population of the sheep reach 900? Give your answer to the nearest month.
, where P t is measured in months. When does the population of the sheep reach 900? Give your answer to the nearest month.

