Raymond J. answered • 02/17/21
Patient with Ability to Explain in Many Ways
This looks fairly straightforward.
F(t) = (t2 + 1)/(1 + t) gal/min
E(t) = (ln(t + 7))/(t + 2) gal/min
At t = 12 min
F(12) = ((12)2 + 1)/(12 + 1) = (144 + 1)/(13) = 145/13 gal ≈ 11.15 gals
So after 12 minutes, 11.15 gallons enters the tank.
E(12) = ln(12 + 7)/(12 + 2) = [ln(19)]/(14) ≈ 0.21 gals.
After 12 minutes, 0.21 gallons has emptied out of the tank.
F(12) - E(12) = 11.15 - 0.21 = 10.94 ≈ 11 gallons is in the tank after 12 minutes.
Katelyn Y.
I got ~61 gallons06/04/21


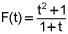 , and at the same time empties out at the rate
, and at the same time empties out at the rate 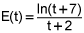 , with both F(t) and E(t) measured in gallons per minute. How much oil, to the nearest gallon, is in the tank at time t = 12 minutes? You must show your setup, but can use your calculator for all evaluations.
, with both F(t) and E(t) measured in gallons per minute. How much oil, to the nearest gallon, is in the tank at time t = 12 minutes? You must show your setup, but can use your calculator for all evaluations.


Katelyn Y.
Incorrect because F(t) and E(t) are rates with the units gal/min so you can't just plug in the time value to find the gallons. You need to take the integral of both equations from 0 to 12 then subtract.06/04/21