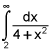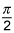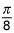Evaluate the integral from 2 to infinity of the quotient of 1 and the quantity 4 plus x squared dx

Question

Evaluate  

A
B
C	π
D	Does not converge

Answer 1

The way to evaluate an improper integral, like this one, is to just use a dummy variable (which we'll call a in this case) and take the limit.

In this case what we do is say that this integral is equivalent to: lim _a→∞∫₂^adx/(4+x²)

The integral itself is just a simple trig sub: 1/4 * lim _a→∞∫₂^adx/(1+x²/4)

In this case, we let x/2 = tan y, then x = 2 tan y and dx = 2 sec² y dy. We also need to change the bounds on this integral. Since we are going from x = 2 to x=a and we know x = 2 tan y, we can change the bounds by saying 2 = 2 tan y and thus 1 = tan y, so y = π/4 on the bottom and a = 2 tan y, so a/2 = tan y, so y = tan^-1(a/2) = arctan (a/2) for the top bound.

The integral becomes 1/4* lim _a→∞∫_π/4^arctan(a/2) 2sec²y dy/(1+ tan² y)

= 1/4* lim _a→∞∫_π/4^arctan(a/2) 2sec²y dy/(sec²y)

After cancelling out, this integral then becomes: 1/4* lim _a→∞∫_π/4^arctan(a/2) 2 dy

= 1/4 * lim _a→∞ [_π/2^arctan(a/2) 2y]

= 1/4 * lim _a→∞ [2 arctan(a/2) - π/2]

= 1/4 *[π - π/2] = π/8, which is c.

Answer 2

^{∞ b b}

∫ dx / 4 +x² = lim b→∞ ∫ dx / 4 +x² = lim b→∞ 1/2 tan ^-1( x/2) Ι

_{2 2 2}

= lim b→∞ 1/2 [ tan ^-1( b/2) - tan ^-1( 2/2) ]

= 1/2 [ tan ^-1 ∞ - tan ^-1( 1) ] = 1/2 [ π/2 - π/4 ] = π / 8

Answer 3

Area = ∫1/(4+x²)dx = ∫1/(2²+x²)dx = tan^-1(x/2)/2 |₂^∞ = (π/2)/2 - (π/4)/2 = 2π/8 - π/8 = π/8

Answer B