Answer is
| B | F(x) = x2 + 4x - 12 |
The fundamental theorem of calculus part 1
d/dx [ ∫2x f(t) dt ] = f(x)
F(x) = ∫2x ( 2t+4) dt
= 2 t2 /2 + 4t Ιx2
= t2 + 4t Ιx2
= ( x2 + 4 x ) - ( 22 + 4* 2)
= x2 + 4 x- 12
Cameron L.
asked • 02/02/21Use the graph of f(t) = 2t + 4 on the interval [-4, 6] to write the function F(x), where 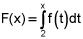
| A | F(x) = x2 + 6x |
| B | F(x) = x2 + 4x - 12 |
| C | F(x) = x2 + 4x - 8 |
| D | F(x) = x2 + 8x - 20 |
Answer is
| B | F(x) = x2 + 4x - 12 |
The fundamental theorem of calculus part 1
d/dx [ ∫2x f(t) dt ] = f(x)
F(x) = ∫2x ( 2t+4) dt
= 2 t2 /2 + 4t Ιx2
= t2 + 4t Ιx2
= ( x2 + 4 x ) - ( 22 + 4* 2)
= x2 + 4 x- 12
Get a free answer to a quick problem.
Most questions answered within 4 hours.
Choose an expert and meet online. No packages or subscriptions, pay only for the time you need.