
Justine R. answered • 09/22/20
Your success is my success!
1] Rewrite the equation so that we have variables of x with all exponents:
-4x3 - x2 + 0x - 12 ÷ (x + 4)
2] Next, set the component you are dividing by equal to zero and solve for x:
(x+4) = 0 and so after solving we have: x = -4
3] Now we need to perform synthethic division:
First write out -4 (from Step 2 above) and the numbers in front of the variables as well as the constant -12:
-4 || -4 -1 0 -12
We next bring down the second -4 and multiply the -4 from Step 2 by it to get 16. Once we have that we place it under the next number which is -1.
-4 || -4 -1 0 -12
-4
-4 || -4 -1 0 -12
16
-4
Now add the -1 and 16 to get 15 and place underneath.
-4 || -4 -1 0 -12
16
-4 15
Now multiply -4 by 15 to get -60 and place under the next number which is zero and then add 0 and -60. This is the general process we will repeat until the last number.
-4 || -4 -1 0 -12
16 -60
-4 15
Then once we repeat the above process two more times we get:
-4 || -4 -1 0 -12
16 -60 240
-4 15 -60 228
4] The last number on the bottom far right corner is our remainder (228).
5] Now we take our original equation from above ( -4x3 - x2 + 0x - 12 ) and replace the numerical values with our new ones that we acquired ( -4, 15, -60 and 228) to get:
-4x3 + 15x2 - 60 + 228
6) Next, since we are diving the whole thing by (x+4) we divide by x for each variable in the equation to get:
-4x2 + 15x - 60 + 228
Since our remainder (228) is not zero we divide it by (x+4) and leave it in that format.
-4x2 + 15x - 60 + (228 / (x+4))
This is our quotient and our remainder is 228.
I hope you found this helpful!


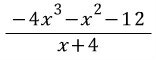



Ooyeon O.
Thank you09/24/20