Find the magnitudes of T

Question

A traffic light weighing 19 pounds is suspended by two wires as shown in the figure below. Find the magnitude |T₁| of the tension in wire AC, and the magnitude |T₂| of the tension in wire AB. (Round your answers to the nearest whole number.)

Answer 1

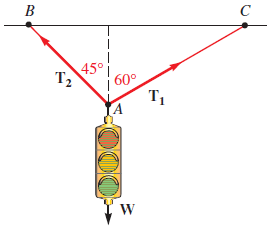
Divide T₁ and T₂ into their x & y component vectors:

T_1x = T₁ (sin60) T_2x = T₂ (sin45)

T_1y = T₁ (cos60) T_2y = T₂ (cos45)

Note that the net force in the horizontal (i.e., x) direction is 0, since the traffic light is not accelerating horizontally. Thus,

T_1x = T_2x

T₁ (sin60) = T₂ (sin45)

Additionally, the traffic light is not accelerating vertically (i.e., in the y direction), either. There are three forces acting in the y-direction: T_1y , T_2y , & the force of gravity on the traffic light (i.e., its weight). Since there is no acceleration in the y-direction, the sum of the three forces is 0.

∑F_y = T_1y + T_2y + (-19 lbs) = 0

T_1y + T_2y = 19 lbs

T₁ (cos60) + T₂ (cos45) = 19 lbs

At this point, we have found 2 equations describing the relationship between 2 variables (in bold), so we are ready to begin solving for them.

T₁ (sin60) = T₂ (sin45) T₁ (cos60) + T₂ (cos45) = 19 lbs

T₁ = T₂ (sin45) / (sin60)

T₁ = T₂ (0.816) T₂ (0.816)(cos60) + T₂ (cos45) = 19 lbs

T₂ (0.408) + T₂ (0.707) = 19 lbs

T₂ (1.155) = 19 lbs

T₂ = 17.04 lbs

Now that we've found T₂, we can go back to the first equation and find T₁.

T₁ = T₂ (0.816)

T₁ = (17.04 lbs)(0.816)

T₁ = 13.90 lbs