Given angle a equals 90 degrees and angle b equals 90 degrees then prove that angle a and angle b are right angles

Answer 1

Given angle a equals 90 degrees and angle b equals 90 degrees then prove that angle a and angle b are right Angles

Direct Proof  - A proof in which the conclusion is drawn directly from previous conclusions, starting with the first statement.

Geometric Proof  - A step-by-step explanation that uses definitions, axioms, postulates, and previously proved theorems to draw a conclusion about a geometric statement. There are two major types of proofs: direct proofs and indirect proofs.

Indirect Proof  - A proof in which a statement is shown to be true because the assumption that its negation is true leads to a contradiction.

Types

solution

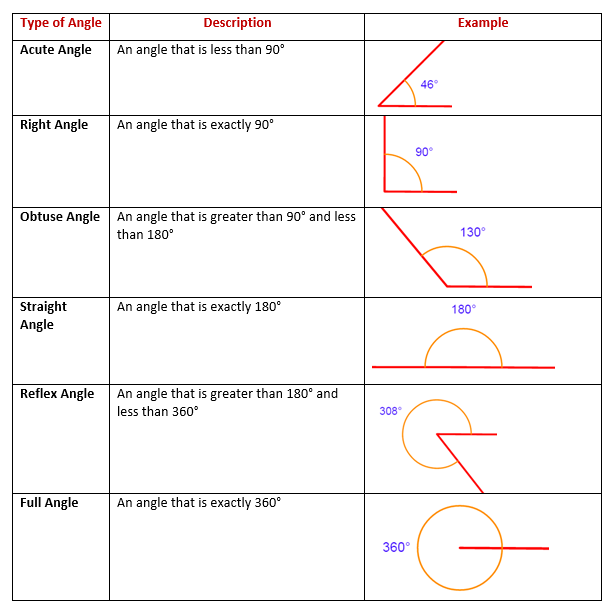
In geometry angles can be classified according to the size of the angle. Proving Angles Are Congruent

Geometry

1. Proving Segment and Angle Relationships
2. Exploring Midpoints
3. How Many Midpoints Are There?
4. Proving Angles Are Congruent
5. Using and Proving Angle Complements
6. Using and Proving Angle Supplements

Two angles are congruent if they have the same measure. You already know that when two lines intersect the vertical angles formed are congruent. You have also seen that if ∠A and ∠B are both 90°. There are other angle relationships to explore.

https://www.wyzant.com/resources/lessons/math/geometry/lines_and_angles/angle_theorems

Brielfy a mathematical statement is a sentence which is either true or false. ... For example ``The square root of 4 is 5" is a mathematical statement (which is, of course, false). In mathematics we use language in a very precise way, and sometimes it is slightly different from every day use.

Given takings into account

m stands measure of an angle

∠ stands for angle

STATEMENT REASON

∠ A = 90° Given

∠ B = 90° Given

m∠ A = m∠ B Substitution Property of Equality

m∠ B = m∠ A Substitution Property of Equality

m ∠ A = m ∠ A Algebra

∠ A is 90° Definition of Right Angle