In attempt to win a car, Jacob will flip a coin up to six times. If the coin lands on "heads" six times in a row, Jacob wins. If the coin lands on "tails", the game is over.

Question

In attempt to win a car, Jacob will flip a coin up to six times. If the coin lands on "heads" six times in a row, Jacob wins. If the coin lands on "tails", the game is over. His probability of winning will double after each successful flip, as shown in the table below.

Which exponential function models Jacob's probability of winning after t successful flips?

A. f(t) = 2 ^(t-6)

B. f(t) = 2 ^(6-t)

C. f(t) = 6 ^(t-2)

D. f(t) = 6 ^(2-t)

I think the answer is either A or D

Answer 1

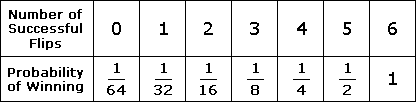
The probability of getting a head when flipping a fair coin is 1/2. Since a particular flip of a coin is not affected by another flip of that same coin, then two coin flips are independent events. This means that the probability that both of the coin flips result in heads is just the multiplication of their individual probabilities. So the probability of getting two heads on two flips of the same fair coin is (1/2)^2 = 1/2 * 1/2 = 1/4. We can then reason that the probability of getting t heads on t flips of the same fair coin is (1/2)^t.

In this particular case of six flips, the probability of getting six heads on six flips is

(1/2)^6 = 1/2 * 1/2 * 1/2 * 1/2 * 1/2 * 1/2 = 1/64

But the question does not ask what the probability is of getting t heads if the coin is flipped t times, but rather asks what is the probability that the remaining flips are all heads after t successful flips. So after t successful flips there are 6-t flips left. Then the equation that models this is 1/2^(6-t)

This means that none of the listed answers are correct.