Calculate ΔG for the reaction below at 25°C when 1.00 atm of A and 8.20 atm of B are present.

Question

Calculate ΔG for the reaction below at 25°C when 1.00 atm of A and 8.20 atm of B are present. 

ΔGº = +5.44 kJ/mol for this reaction.

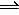A(g)2B(g)

in KJ/mol

Answer 1

For this problem, we must first consider the overall equation that can lead us to our answer. That would be:

ΔG = ΔGº + RT * ln(Q)

We are already given that ΔGº = +5.44 kJ/mol and T = 25 °C, and we know that this ideal gas constant, R, is equal to 8.3145 J*mol^-1*K^-1. For ease of calculation, I will put these values in terms of Joules and Kelvin. Knowing that 1 kilojoule is equal to 1000 joules and that to convert from degrees Celsius to Kelvin we must just add 273, we get:

ΔGº = +5.44 kJ/mol

ΔGº = +5,440 J/mol

T = 25 °C

T = 298 K

Our last obstacle with this problem is finding the reaction quotient, Q. To do that, we must first convert the pressures of each of our molecules to concentrations. To do that we simply use the equation PV = nRT. Please note that in this case, since the units are different R is actually equal to .08206 atm*L*mol^-1*K^-1. Using algebra, we can rearrange the equation like so:

P/RT = n/V

Since n/V is given in the units mol/L, this number actually gives us the exact molarity of our substances. Thus, for both A and B we can perform math like so to calculate their concentrations:

[A] = 1.00/(.08206)(298)

[A] = .0409 M

[B] = 8.20/(.08206)(298)

[B] = .335 M

Using these values along with the equation for the chemical reaction listed above, we can then find the reaction quotient, Q, like so:

Q = [B]²/[A]

Q = (.335)²/(.0409)

Q = 2.750

Using the initial equation we had, we can then plug in our numbers to find our ΔG value:

ΔG = ΔGº + RT * ln(Q)

ΔG = 5440 J/mol + (8.3145 J*mol^-1*K^-1)(298 K) * ln(2.750)

ΔG = 5440 J/mol + 2506 J/mol

ΔG = 7946 J/mol

ΔG = 7.95 kJ/mol