These 2 equations can help you solve these problems:
1) ∆G° = -RTlnK
2) ∆G = RTln[Q/K]
a) Where R is gas constant 8.314JK^-1mol^-1,. T is temperature, and K is equilibrium constant.
Since this is ∆G° it refers to standard conditions. Standard conditions are 1M, 1atm, For both sides products and reactants, 25° or 298 K. The ln is the natural log. So evaluating the equation with these conditions:
∆G° = -(8.314)298ln[1/1]
Since the natural log or ln of 1 is 0, everything is 0 based on the scenario in part a. So ∆G° = 0 at equilibrium neither product nor reactants are favored.
b) ∆G = RTln[Q/K]
Since this is not indicating standard conditions you can use the temperature in the problem, 298K.
(8.314)298ln[12/1]. When ∆G° = 0,. K= 1. So evaluating this equation gives:
(8.314)298ln[12/1] = 6156.5J. In the units of Gibbs free in kJ we just divide this number by 1000 or multiply by the equivalency 1000J = 1kJ
Dividing by 1000 gives ∆G = 6.1565 kJ/mol
c) use the same equation:
∆G = RTln[Q/K]. = (8.314)298ln[0.300/1] = -2982.9 J or 2.9829 kJ/mol
d) Now given ∆G, solve for Q:
∆G = RTln[Q/K = -4.10kJ/mol= (8.314)298ln[Q/1]
-4.10/(8.314)298 = ln[Q]
e^(-4.10/(8.314)298) = e^Q
Q = 0.99835. or 0.998
This makes sense because it is similar to the numerical expression, Q value in part C of this problem.

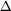 G when Q, the [F6P]/[G6P] ratio, equals 12.0.
G when Q, the [F6P]/[G6P] ratio, equals 12.0.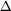 G =
G = 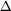 G0 + RTlnQ
G0 + RTlnQ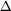 G = 1.67 kj/mole + 8.314 x 298C x ln 12.0 = 7.83 kj/mole
G = 1.67 kj/mole + 8.314 x 298C x ln 12.0 = 7.83 kj/mole G when Q = 0.300.
G when Q = 0.300. G =
G =  G0 + RTlnQ = 1.67 kj/mole + 8.314 x 298 x ln 0.300 = - 1.31 kj/mole
G0 + RTlnQ = 1.67 kj/mole + 8.314 x 298 x ln 0.300 = - 1.31 kj/mole G = -4.10 kJ/mol.
G = -4.10 kJ/mol.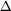 G =
G = 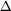 G0 + RTlnQ , -4.10 kj = 1.67 kj/mole + 8.314 x 298 x lnQ
G0 + RTlnQ , -4.10 kj = 1.67 kj/mole + 8.314 x 298 x lnQ


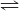 F6P
F6P


Anthony T.
I see another tutor has a different approach. Can you let me know the correct answer when you have it?04/25/22