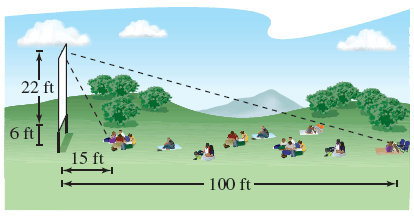
Aneesh C. answered • 01/17/21
Credentialed Math Teacher and Academic Math Tutor
Hi Aerin,
The key to answering both parts of this question is that for right triangles, we can find an unknown angle as long as we know the lengths of two of its sides.
Recall that:
sin(θ) = opposite / hypotenuse
cos(θ) = adjacent / hypotenuse
tan(θ) = opposite / adjacent
a) Since we want to find out the angle of elevation, here's how we can set up the equation to find this angle:
tan(θ) = 28/15 --> tan-1(28/15) = θ --> θ = 61.82º from a distance of 15 feet
tan(θ) = 28/100 --> tan-1(28/100) = θ --> θ = 15.64º from a distance of 100 feet
b) For this part, we know the angle of elevation but we do not know how far away the person is, i.e. we do not know the length of the adjacent side of this angle. However, we can still use the tangent formula as follows:
tan(32º) = 28/x
x = 28 / tan(32º) = 44.8 feet away from the screen