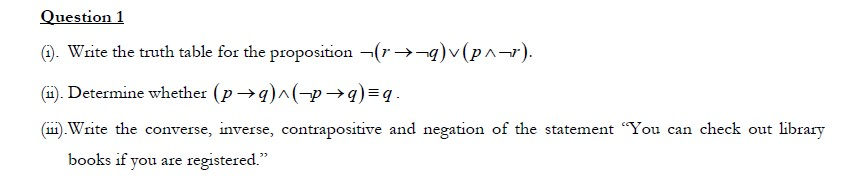Discrete Mathematics Questions

Question

Answer 1

(1)

i) P q r ~q ~r R->~q p and ~r ~(r->~q) final

============================================================

T T T F F F F T T

T T F F T T T F T

T F T T F T F F F

T F F T T T T F T

F T T F F F F T T

F T F F T T F F F

F F T T F T F F F

F F F T T T F F F

ii) (p->q) and ( ~p->q) =

(~p v q) and (p v q) = <-- identity of p->q

q v (~p and p) = <-- reverse distributive

q v F =

q

or truth table says:

p q ~p p->q ~p->q final

T T F T T T

T F F F T F

F T T T T T

F F T T F F

and the final column is the same as Q

iii) if you are registered, then you may check out the library books

p=registered q= allowed to check out the library books

converse q->p , if You can check out library books then you are registered

inverse ~p->~q, if you are not registered, then you may

not check out the library books

contrapositive ~q -> ~p, if you may not check out the library books,

then you are not registered

negation: ~(p->q) = ~(~p v q) = p and ~q

you are registered and you may not check

out library books

(2)

(i) ~A

(ii) for all S, A holds true

(iii) if not A, then not S

(iv) S holds for all empty sets

(3)

(i) x<y is given

then x+x < x+ y <--- adds x to both sides

2x < x+y <-- combines like terms

Likewise, since x<y, x+y < y+y

x+y < 2y

So then 2x < x+y < 2y

DIvideds everything by 2: x < (x+y)/2 < y

(ii) counterexample: -3 is an integer. (-3)^3 = -27

but -3 > -27

this holds for negative integers in general

(iii) suppose x>y...

then x-y>0, so |x-y|=x-y

so then (x+y+|x-y|) = x+y+x-y =2x,

half of which is x, which is the max..

suppose y>x...

then x-y<0, so |x-y| = -(x-y) = y-x

so then (x+y+|x-y|) = x+y+y-x = 2y,

half of which is y, which is the max.

suppose x=y...

then x-y=0, so |x-y| = 0.

so then (x+y+|x-y|) = x+y + 0 = x+y = 2N, where x=y=N.

half of which is N = x = y which is the max.

(iv) if x>0, then |x|=x. Then |x|-x = x-x >= 0, so |x|>=x.

if x<0, then |x|=-x. Then |x|-x = -x-x = -2x>=0, so |x|>=x.

The statement clearly holds when x=0, and left for you to verify.

(v) Given : 3n+5 is even; Prove n is odd

It's easier to go by contraction, as directly results in fractions.

Suppose n is even. Then n = 2x for integer x.

So then:

3n+5 = 3(2x)+5 <-- substitution

= 6x+5 <-- combines like terms and distributive

= (6x + 4) + 1 <-- associative

= 2(3x+2)+1 = <--- reverse distributive

= 2 T + 1 for integer T=3x+2 <-- closure property of integers

over addition and multipication

Therefore 3n+5 is odd, which is a contradiction.

(4) (i) use Venn Diagram

(ii) use Distributive

(iii) use DeMorgan's