Using the initial partial pressure of A2 and the ideal gas law, you can find the initial moles of A2
PV = nRT
n = (2.56 atm)(1 L)/(0.08206)(298 K) = 0.105 mol A2 = 0.105 mol B2
Using Avogadro's number, you can find the moles of A2 at equilibrium. The moles of A2 and B2 are the same since they started at the same partial pressure and are used in equimolar amounts.
(2.82e13 molecules) * (1 mol/6.02e23 molecules) = 4.68e-11 moles A2 = moles B2
Based on the reaction, 2 moles of C are formed for each mole of A2 used.
0.105 mol A2 initial - (4.68e-11 mol A2 at equilibrium) = 0.104999 mol A2 used
0.104999*2 = 0.209998 mol C at equilibrium
To find the equilibrium constant, K, use the following equation, based on the reaction coefficients. These are the concentrations of the components (moles/L), and all the volumes are 1.0 L, so these can be ignored.
K = [C]2/([A2][B2]) = (.209998)2/((4.68e-11)(4.68e-11)) = 2.013e19
The Gibbs free energy (ΔG) can be calculated from the following equation:
ΔG = - RTlnK = - 8.314 J/mol/K * 298K * ln(2.013e19) * 0.209998 mol C = -23,126 J = -23.1 kJ in terms of C produced
To find the entropy (ΔS), use the following equation:
ΔG = ΔH - T*ΔS
ΔS = (ΔG - ΔH)/(-T) = (-23.1 kJ - (-104.3 kJ))/(-298 K) = -0.27 kJ/K = -272 J/K
Note: It seems odd that ΔH is given in kJ and not kJ/mol for the reaction. You may need to multiply ΔH by 0.20998 mol in the above equation, giving an answer of ΔS = 4 J/K.


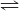 2 C(
2 C(


