Consider the following figure.

Question

Calculate the current in each resistor if a potential difference of 74.0 V is applied between points a and b.

(R= 18.0Ω)

I(4.00 Ω):

I(7.00 Ω):

I(18.0 Ω):

I(9.00 Ω):

Answer 1

Hi Charlotte,

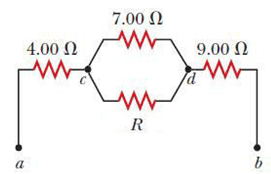
First Step: Combine resistors into one total resistance value using the rules of parallel and series resistors.

I. Let's start by combining the parallel resistors, 7Ω and 18Ω .

1/7 + 1/18 = 1/Rt (Rt is denoting the combined resistance of the parallel resistors)

Solving for Rt, we get...

=> Rt = 126/25 Ω

II. Now that we have combined the parallel resistors, we are left with three resistors in series: 4 Ω,

126/25 Ω, and 9 Ω.

Summing for total resistance of the series circuit:

R_total = 4Ω + 126/25Ω + 9Ω = 451/25 Ω

Second Step: From the previous step we combined all the resistors into one total resistance, Rtotal.

We will now use this total resistance to find the total current in the circuit.

Using Ohm's law:

V = IR

74 V = I_total * (451/25) Ω

=> I_total = (1850/451) A

Third Step: There are many methods for solving for the current across each resistor. Here are two examples.

Method 1: Concepts of Circuits and Nodal Analysis

Concepts

a. Current across resistors in series is the same.

b. Sum of branches of current at a node sum to zero

c. Voltage drop across resistors in parallel is the same

The 4 Ω and 9 Ω resistors will experience the same current, equal to the I_total calculated earlier. This can be deduced by the series circuit analysis done previously and concept a.

Looking at the first node of the circuit, current going into the node is the same as the current going out. So, current across 4 Ω resistor is equal to the sum of the individual currents across the 7 Ω and 18 Ω resistors (*note that we must treat the current of each parallel resistor individually).

We can translate this to equation form. (I_total is the the total current found in the previous step and is across the 4 Ohm resistor, i2 is the current across the 7 Ohm resistor and i3 is the current across the 18 Ohm resistor)

I_total = i1 + i2 (eq 1)

From concept c above, we can formulate the following equation using Ohm's Law:

i1 * (7 Ω) = i2 * (18 Ω) (eq 2)

Now we can solve for i1 and i2 using equations 1 and 2:

(18/7) * i2 + i2 = I_total

i2 = I_total/(1+(18/7))

=> i2 = 1850 A /(451 * (1+(18/7))) = 1.14855 A

=> i1 = (18/7) * i2 = 2.9534 A

Method 2: Kirchoff's Current Analysis

This method is a fairly robust way to solving any circuits problem and an excellent tool to have. I have linked a video series below that may be help you. There some other helpful videos in there as well.

https://www.khanacademy.org/science/physics/circuits-topic/circuits-resistance/v/ee-kirchhoffs-current-law

Please let me know if you have any questions or concerns.

Answer 2

R = 4 + 7·18/25 + 9 = 18.04 Om

I(4 Om) = I(9) Om)= 74/18.04 = 4.10 A

I(7 OM) = 4.10·5.04/7 = 2.95 A

I(18 Om) = 4.10·5.04/18 = 1.15 A