Why or where was the number 9 introduced in the answer to part b?

Question

A cylinder (round can) has a circular base and a circular top with vertical sides in between. Let r be the radius of the top of the can and let h be the height. The surface area of the cylinder, A, is A=2πr2+2πrh

 (it's two circles for the top and bottom plus a rolled up rectangle for the side). 

 

Part a: Assume that the height of your cylinder is 6

 inches. Consider A as a function of r, so we can write that as A(r)=2πr2+12πr. What is the domain of A(r)? In other words, for which values of r is A(r)

 defined?

 

Part b: Continue to assume that the height of your cylinder is 6

inches. Write the radius r as a function of A. This is the inverse function to A(r), i.e to turn A as a function of r into. r as a function of A.

ANSWER:

Part a)

Can "r" by a negative number? No, although negative numbers are defined in math, real cylinders can't have a negative radius. Can "r" be zero? No, if it were, there would be no cylinder. It also makes sense that the upper limit would be restricted as well since, on earth, you can't have an infinitely large radius but it's really hard to define what's too big so I'd probably just say the domain is r > 0 (this can be written in many formats).

Part b)

A = 2πr²+12πr

A/(2π) = r² + 6r

A/(2π) + 9 = r² + 6r + 9

A/(2π) + 9 = (r + 3)²

√(A/(2π) + 9) = r + 3

r = √(A/(2π) + 9) - 3

r(A) = √(A/(2π) + 9) - 3

(Notice I only used the positive square root since we are being asked to find a function and +/- would not yield a function. Besides, we already stated that r > 0.)

Part c)

In part b we found r(A) = √(A/(2π) + 9) - 3

so r(150) = √(150/(2π) + 9) - 3 = √32.873 - 3 = 5.73 - 3 = 2.73 inches

Answer 1

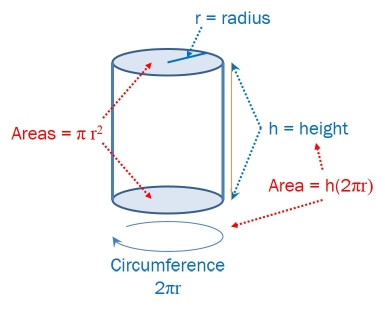
Starting with A = 2πr²+2πrh, plug in h = 6 to get:

A = 2πr²+12πr

This is now the area as a function of radius so:

A(r) = 2πr²+12πr

To convert this to radius as a function of area, we need to flip things around. First step, divide by 2π:

A/(2π) = r² + 6r

Now, complete the square. To determine the value to add to both sides that will allow the right side to be written as a perfect square, divide the coefficient of "r" (which is "6") by 2 and then square the result. 6/2 = 3 and 3 squared is 9. So add 9 to both sides to get:

A/(2π) + 9 = r² + 6r + 9

Now, write the right hand side as a square:

A/(2π) + 9 = (r + 3)²

Now take the square root of both sides:

√(A/(2π) + 9) = r + 3 Note: the "math" way to do this would be to add a "±" but that would NOT result in a function so we choose just the positive.

Now subtract 3 from both sides to get:

r(A) = √(A/(2π) + 9) - 3