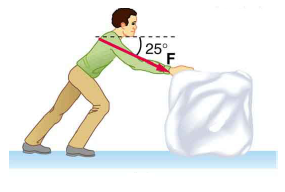
Daniel B. answered • 09/22/21
A retired computer professional to teach math, physics
Let
m = 43 kg be the mass of the ice block,
α = 25° be the angle of the force F,
H = Fcos(α) be the horizontal component of the force F,
V = Fsin(α) be the vertical component of the force F,
s = 0.1 be the coefficient of static friction,
d = 0.03 be the coefficient of dynamic friction,
g = 9.81 m/s² be gravitational acceleration,
a (to be calculated) be the acceleration of the block once it starts moving.
Friction is due to the weight, mg, of the block plus the additional vertical force V.
Therefore the total force of static friction is
(mg + V)s
The minimal horizontal force, H, to overcome the force of friction must satisfy
H = (mg + V)s
Substituting H and V
Fcos(α) = (mg + Fsin(α))s
Solving for F
F = mgs/(cos(α) - sin(α)s) (1)
Substituting actual numbers
F = 43×9.81×0.1/(cos(25°) - sin(25°)×0.1) = 48.82 N
Now for the acceleration:
Like the force of static friction, the total force of dynamic friction is
(mg + V)d
So the net horizontal force acting on the block of ice is
H - (mg + V)d
By Newton's second law
H - (mg + V)d = ma
Solving for a
a = (H - (mg + V)d)/m = (H - Vd)/m - gd
Substituting H and V
a = (Fcos(α) - Fsin(α)d)/m - gd = (cos(α) - sin(α)d)F/m - gd (2)
At this point you could substitute the computed F = 48.82 N and get the acceleration a.
But I will substitute the symbolic solution (1) to illustrate the point that the
acceleration a does not depend on the mass m.
Substituting (1) into (2)
a = ((cos(α) - sin(α)d)mgs/(cos(α) - sin(α)s)) / m - gd
= gs(cos(α) - sin(α)d)/(cos(α) - sin(α)s) - gd
Notice that the minimal force F to overcome static friction does depend on the mass m,
but the acceleration a does not.
Substituting actual numbers
a = 9.81×0.1×(cos(25°) - sin(25°)×0.03)/(cos(25°) - sin(25°)×0.1) - 9.81×0.03 = 0.72 m/s²