Optimization question; fencing problem

Question

A rancher has 560 feet of fencing with which to enclose two adjacent rectangular corrals (see figure). What dimensions should be used so that the enclosed area will be a maximum?

x = ?

y = ?

1. 
   

any guidance will be much appreciated, thank you in advance.

Answer 1

Net perimeter is 560 ft

P = 560

P = 4x + 3y

560 = 4x + 3y

y = (560 -4x)/3

Area of the fence for rectangle

A = base * height = 2x * y

A = 2xy

sub in y for Area expression

A = 2x * (560 -4x)/3

A = (1120x /3) -( 8x^2 /3)

Now optimize by Solving for dA/dx = 0

(1120-16x)/3=0

x= 70 ft

solve for y

560 = 4(70) + 3y

y= (560-280)/3

y= 280/3 ft

Answer 2

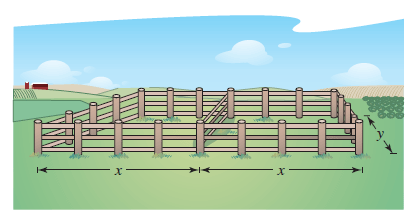
Hello, Ta. To get started, think about how you can get an expression for the perimeter. The problem tells you what the total perimeter is; now, express it in terms of x and y. There are 4 segments of length x and 3 segments of length y, so the perimeter is 4x + 3y = 560 feet. Further, the area is just length time width: 2x*y. We want to find either the x or y such that the area is maximal. However, right now there are two variables, and we would rather have just one. Luckily, we know another equation, and we can choose to write it in terms of x or y. I will choose y: y = (560-4x)/3. Thus, we know that the area is 2x*((560-4x)/3). At this point, you can differentiate with respect to x and set the derivative equal to 0. Recall that maxima and minima occur when the derivative is 0. So, when you solve for x, you will find the value(s) of x that maximize or minimize the area. To verify that the value yields a maximum, use either the first derivative or second derivative test. Once you find the right value for x, plug it into your perimeter equation and solve for y. Let me know if you have any questions!