Use​ Green's functions to solve the given boundary value problem.

Question

Use​ Green's functions to solve the given boundary value problem.

y'-y=6x; y(0)=0, y(2)=0

Answer 1

Step 1

The given function:

y'-y=6x

The initial conditions are,

y(0)=0, y(2)=0

The general solution of the above function is,

y(x)=A cos x + B sin x+6x  

Using Green's function for the above solution:

G(x, s)=A(s) cos x + B(s) sin x+6x -  equation 1

That is,

 

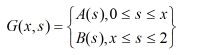
Step 2

Apply initial conditions to the above solution,

At y(0)=0;

G(0,s)=A(s) cos 0 + B(s) sin 0+6(0)=0

[cos 0=1; sin 0=0]

G(0,s)=A(s) (1)=0

  A(s)=0

G(0,s)= B(s) sin x

At y(2)=0;

G(2,s)=A(s) cos (2) + B(s) sin (2)+6(2)=0

[A(s)=0]

G(2,s)=B(s) (0.0349)=-12

  B(s)=-343.8395

G(2,s)=-343.8395 sin x+6x

Substitute A(s) and B(s) value in equation 1,

G(x, s)=-343.8395 sin x+6x

Then the solution is,

y(x)=G(x, s)=-343.8395 sin x+6x