Tom K. answered • 04/20/21
Knowledgeable and Friendly Math and Statistics Tutor
I believe I answered either this exact problem or a similar one before. As f'(x) is negative throughout the interval, we know that the maximum of all of these is the left endpoint (5) and the minimum is the right endpoint (3). Since the function is convex (f''(x) > 0), the actual area (1) is less than the trapezoidal rule (4) and the midpoint (2) is less (just think about where the function is located versus the endpoints and where the function is located at the midpoint versus a line between the endpoints). Thus, we are left with the function at the midpoint versus the convex function. Then, consider the trapezoid formed using the function value and derivative at the endpoint. As the function is convex, the function will be above this line (the derivative is less than the slope of the line to the left of the endpoint, and greater than the slope of the line to the right), so the area of the function is greater.
Thus, 3 < 2 < 1 < 4 < 5
b < c < e < d < a
3b, 2c, 1e, 4d, 5a


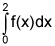



Sreeram K.
Correct! Thank you so much!04/20/21