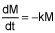The rate of decay in the mass

Question

The rate of decay in the mass, M, of a radioactive substance is given by the differential equation  , where k is a positive constant. If the initial mass was 100g, then find the expression for the mass, M, at any time t. 

A)M = e^-kt

B)M = 100 e^-kt

C)M = 100 e^kt

D)M = 100ln(kt)

I believe the answer is B

Answer 1

You're correct that the answer is B!

Since you're right, I'll go relatively quickly through my explanation just to show the correct steps you'd take to solve this problem:

Separate dM/dt = -kM as such:

(1/M) × dM = -k dt

Integrating both sides, we get:

ln(M) = -kt + C

∴ M = e ^{-kt + C}

We can write it as M = e^-kt × e^C. Let's call e^C = c₁

M = c₁e^-kt. We know that the initial mass is 100 g: At t = 0, M = 100!

100 = c₁e^-k(0)

100 = c₁

∴ Our particular solution is M = 100e^-kt, answer b!