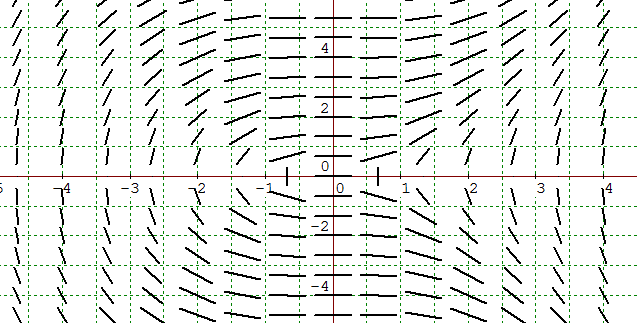
One of the ways to figure out which differential equation is the correct one is to take several points and plug them into each equation. You can also sometimes just tell from the picture if the equation is consistent or not. For example, if we look at the field below the x-axis all slopes seem to be negative except at 0. Anything above the x-axis seems to be positive except at 0.
Seeing that on the picture we know that choice d) is out since x^2/y^2 will never be negative. We can also get rid of b) x/y as an option since if we look at the third quadrant we have negative slopes which is impossible for x/y to have since a negative number divided by another negative number is positive. So now we are left with a) and c).
To check the last two options let's plug in some points. Looking at point (2,4), by the picture we can guess that the slope is about 3/4 so y'≈3/4 at (2,4). Plugging the point into both equations for a) we get 2/42 = 2/16 = 1/8
for c) we get 22/4 = 4/4 = 1. Nothing really conclusive yet so let's try another point (4,4) where y' looks to be about approximately 4 so y'≈4 at (4,4). Plugging that in we get for a) 4/42=4/16=1/4 and for c) 42/4 = 16/4 = 4. It looks like option c) is our answer but just to be extra sure I am going to check a third point. Looking at point (2,-2), y'≈-2 so for a) 2/(-2)2 = 1/2 and c) 22/-2 = -2. So option c) is definitely our choice. You could have also noticed that in the fourth quadrant option a) will never be negative since y2 is always positive thus it doesn't match up with picture. But choosing points is a good way to check.
Hope this helps!
(Reminder Note: the dashes are determined to be positive or negative depending on the reading them left to right. That is if the starting point or the left end of the dash is higher than the end of the dash or the right end, the slope is determined to be negative. If the left end of the dash is lower than the right end then the slop is positive.)






Sreeram K.
Correct! Thank you so much!04/20/21