1st, put all your heading into Math angle (0 at x axis and counterclockwise). If you do that then vx = vcos(θ) and vy = vsin(θ) and you do not need to worry anymore about trig functions. (v stands for any vector)
2nd, You have 2 equations (x and y displacement component balances) and two unknowns dc and db:
The resultant is 0 which means the x and y resultants are 0
dax + dbx + dcx = 0 or dacos(θa) + dbcos(θb) + dccos(θc) = 0
Do the same for y
3rd: solve simultaneous equation in db and dc
I answered the 2nd question.
The first is standard:
1) math angles
2) find x and y resultants
3) combined d - sqrt(dx2 + dy2) and θ = tan-1(dy/dx) (add 180 if dx < 0) Redefine angle as a heading.


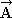 has a magnitude of
has a magnitude of 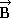 points
points 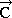 points
points 


