Physics Homework question. please show steps

Question

A 19.8-kg box rests on a frictionless ramp with a 16.3° slope. The mover pulls on a rope attached to the box to pull it up the incline. If the rope makes an angle of 42.8° with the horizontal, what is the smallest force F the mover will have to exert to move the box up the ramp? 

? N

Answer 1

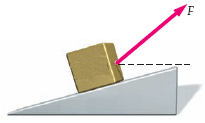
Let

m = 19.8 kg be the mass of the box,

α = 16.3° be the angle of the ramp,

β = 42.8° be the angle of the force,

g = 9.81 m/s² be gravitational acceleration.

The weight of the box, mg, can be decomposed into the sum of two forces:

mg = G_n + G_p

where, the "+" denotes vector addition, and

G_n = mgcos(α) is the force normal to the surface of the ramp, and

G_p = mgsin(α) is the force parallel to the surface of the ramp.

The force G_n would cause friction if there were any, but in this problem we are to ignore that.

The force G_p is the force pulling the box down the ramp and that is the force the mover

must overcome.

Similarly, the mover's force F can be decomposed

F = F_n + F_p

where, the "+" denotes vector addition, and

F_n = Fsin(β-α) is the force normal to the surface of the ramp, and

F_p = Fcos(β-α) is the force parallel to the surface of the ramp.

Just to overcome the downward force of gravity, the mover's force must satisfy

Fcos(β-α) = mgsin(α)

F = mgsin(α)/cos(β-α)

Substituting actual numbers

F = 19.8 × 9.81 × sin(16.3°) / cos(42.8° - 16.3°) = 60.9 N