Michael K. answered • 02/18/21
PhD professional for Math, Physics, and CS Tutoring and Martial Arts
Vector addition is much like polynomial addition in that only like components can be added/subtracted together.
We see we have vectors:
- A = 7.2*i + 4.0*j
- B = 5.0*i + 4.3*j
- C = 6.4*i + 5.9*j
Calculation of D must result in the following truthfulness of the equation...
D + 1*A - 2*B + 3*C = 0
1*A = A = 7.2*i + 4.0*j
-2*B = -10*i - 8.6*j
3*C = 19.2*i + 17.7*j
So D = -A + 2*B - 3*C
D = (-7.2 + 10 - 19.2)*i + (-4.0 + 8.6 - 17.7)*j = -16.4*i - 13.1*j
Calculation of the magnitude is to take the Pythagorian product (sqrt( sum of squares )). So let's do this like a polynomial...
sqrt(D*D) = ||D|| = magnitude
D*D = (-16.4*i - 13.1*j)(-16.4*i - 13.1*j) = 269.96 (i*i) + 214.84 (i*j) + 214.84 (j*i) + 171.61 (j*j)
Now, conveniently, i*j = j*i = 0. These represent "dot-products" and since they are 90 degrees from one another they multiply to 0. However, i*i = j*j = 1 (this is due to the fact the two "axes" align perfectly)
D*D = 269.96 + 171.61 = 441.57. (we had expected D*D to be positive and it is)
||D|| = sqrt(D*D) = 21.01 units. (This is the magnitude)
The rotation of vector D from the x-axis can be found via the tangent of the vector D (j-component/i-component)
tan(θ) = -13.1/-16.4 --> tan(θ) = .799
This yields an angle (θ) of 38.62 degrees, but that implies it is in the first quadrant and both the x (i) and y (j) values are negative, so this must be in the third quadrant and we need to add 180 degrees to our answer to place the vector into the proper quadrant.
Therefore θ = 218.62 degrees from the x-axis (counter-clockwise)



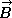
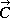
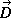 , in unit vector notation, such that
, in unit vector notation, such that 


