tan(θ/2) -sin(θ) = 0
=> sin(θ/2)/cos(θ/2) - 2sin(θ/2)cos(θ/2) = 0
=> sin(θ/2) -2sin(θ/2)cos2(θ/2) = 0, cos(θ/2)≠ 0
=> sin(θ/2) (1- 2cos2(θ/2))=0
This gives you three equations:
sin(θ/2) = 0 or 1-√2 cos(θ/2) = 0 or 1+√2 cos(θ/2) = 0
=>θ/2 = n pi
=> θ = 0 , as θ is in [0, 2𝜋)
1-√2 cos(θ/2) = 0 => cos(θ/2)= 1/√2 = cos(𝜋/4)
=> θ/2 =𝜋/4, 7𝜋/4,..
θ = 𝜋/2
1+√2 cos(θ/2) = 0 => cos(θ/2)= -1/√2 = cos(3𝜋/4)
θ/2= 3𝜋/4
θ = 3𝜋/2
θ = 0, 𝜋/2, 3𝜋/2 Ans


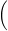 𝜃/2) − sin(𝜃) = 0
𝜃/2) − sin(𝜃) = 0


