Hello Viviana, I'm assuming you are trying to find the value of cos(theta - phi)? If so, this is how I'd go about doing this. For simplicity, let's label those angles x and y, respectively; so that we must find the values of x and y (theta= x, phi=y) .
Firstly, see that tan(y) = -31/2 and y is an angle in the second quadrant. This should be enough to determine y, since for every quadrant, there's only one angle that gives a magnitude of 31/2; this means you just need to find the angle in the second quadrant that gives a tangent value of root(3). You should then find that y= 2pi/3 (i.e, tan(2 pi/3) = -root(3)).
Now, recall that cos(x-y) = sin(x)sin(y) + cos(x)cos(y).
Since we have determined the angle y, and are given cos(x), we may plug those in and see that:
cos(x-y) = sin(x)*root(3)/2 + (5/13)(-1/2).
So what is left to do is find sin(x) and we are done!
To do this, recall that sin2(x) + cos2(x) = 1. Rearranging this gives us that sin(x) = (1 - cos2(x))1/2. Plugging our given value of cos(x) back in gives us:
sin(x) = (1 - (5/13)2)1/2 (a calculator might be useful here)
= (1 - 25/169)1/2
(144/169)1/2
Both of these are perfect squares, so that gives us 12/13. However, the caveat is that x is in quadrant 4, which means that we know its sine value is negative, therefore:
sin(x) = -12/13
Now finally, putting it all together, we get the answer is:
cos(x-y) = -12/13 * root(3)/2 - 5/26 (now simplify)
= -6 root(3)/13 - 5/26
= -(12root(3) +5)/26
(end)


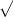 3
3


