Physics Question

Question

Two shuffleboard disks of equal mass, one orange and the other green, are involved in a perfectly elastic glancing collision. The green disk is initially at rest and is struck by the orange disk moving initially to the right at v_Oi = 4.55 m/s

 as in Figure a, shown below. After the collision, the orange disk moves in a direction that makes an angle of θ = 36.0°

 with the horizontal axis while the green disk makes an angle of ϕ = 54.0°

 with this axis as in Figure b. Determine the speed of each disk after the collision.

vof	=	m/s
vgf	=	m/s

Two figures, figure a and figure b, show before and after a glancing collision between two disks.

1. An orange disk is moving horizontally toward the right side with a velocity of vector v_oi, indicated by a rightward horizontal arrow. A dashed horizontal line extends along the same path as the arrow. A green disk is shown at a position to the right of and slightly lower than the position of the other disk.
2. The two disks are shown after they collide.
3. The orange disk is shown to be moving along a diagonal path up and to the right at an angle θ to the horizontal. Its final velocity is shown by an arrow moving diagonally upward and to the right and is labeled vector v_of.
4. The green disk is shown to be moving along a diagonal path down and to the right after collision. The path is at an angle ϕ with the horizontal. Its final velocity is shown by an arrow moving diagonally downward and to the right and is labeled vector v_gf.

Answer 1

Hi Alyssa:

Thank you for providing such a clear question, with all the relevant details.

We know that momentum is conserved => Total momentum before = Total momentum after the collision

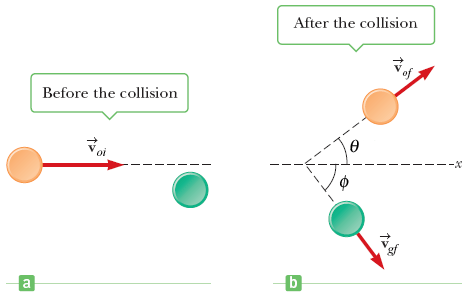
Let the 2 masses be m. We apply conservation of momentum, horizontally and vertically

Total horizontal momentum before = m x 4.55 + 0 = 4.55m . . . . . . . . . . . . . . . . . . . (1)

Total horizontal momentum after = m v_of cos36^o + m v_gf cos54^o . . . . . . . . . . . . . (2)

Equating (1) and (2): v_of cos36^o + v_gf cos54^o = 4.55 . . . . . . . . (A)

Total vertical momentum before = m x 0 + m x 0 = 0 . . . . . . . . . . . . . . . . . . . . . . . (3)

Total vertical momentum after = m v_of sin36^o - m v_gf sin54^o . . . . . . . . . . . . . . . . . (4)

Equating (3) and (4): v_of sin36^o + v_gf sin54^o = 0 . . . . . . . . . . . .. (B)

We now have 2 equations, (A) and (B), in 2 unknowns, v_of and v_gf, so we can solve for the unknowns.

I leave this as an exercise for you. (BTW Do you see the reason for the minus sign in (4)? )