Arthur D. answered • 04/26/20
Mathematics Tutor With a Master's Degree In Mathematics
1+√3
r=√(1^2+√3^2)=√(1+3)=2
tanθ=√3/1=√3, so θ=60°
Z=2(cos60°+isin60°)
5i(1+i)=5i+5i^2=-5+5i
r=√50=5√2
tanθ=5/(-5)=-1, so θ=135°
Z=5√2(cos135°+isin135°)
now multiply the radii and add the angles
z1z2=5√2(cos[9∏/4) +isin[9∏/4])
now divide the radii and subtract the angles
z1/z2=(√2/5)(cos[∏/4]+isin[∏/4])
change to polar coordinates as above
r=√((√2/2)^2+(√2/2)^2)=√((2/4)+(2/4))=√1=1
tanθ=1, so θ=45°
Z^8=1^8(cos[8*45]+isin[8*45])
Z^8=1(cos360°+isin360°)
Z^8=1(1+i*0)
Z^8=1
try the last one
you should get...
Z^18=[√2]^18(cos[18*135]+isin18*135])
18*135=2430, now see how many 360s there are in 2430 and subtract them to get the degree measure


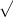 3 i
3 i


