Find the dimensions that give the largest area for the rectangle shown in the figure.)

Question

Its base is on the x-axis and its other two vertices are above the x-axis, lying on the parabola y = k − x2, k = 6. (Round your answers to two decimal places.

height

width

thanks!!

Answer 1

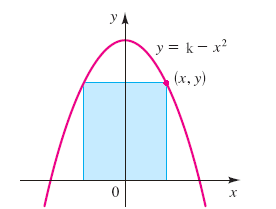
Let's say that the rectangle has the largest area for width = x₁ and height = y₁

So, the rectangle intersects the parabola at (-x₁/2, y₁) and at (x₁/2, y₁)

From the equation of the parabola, we have y₁ = 6 - (x₁/2)²

Therefore, the area z = x₁.y₁ = x₁.( 6 - (x₁/2)² ) = 6x₁ - 1/4 x₁³

For the maximum value of z, we have

dz/dx₁ = 0

d(6x₁ - 1/4 x₁³) / dx₁ = 0

6 - 3/4 x₁² = 0

x₁ = √8 = 2√2

So, y₁ = 4

The rectangle has the largest area for width = 2√2 and height = 4

Answer 2

point (x,y) can be written as (x,6-x^2) because y=k-x^2 and k=6

the base of the rectangle is x+x=2x because of point (x,y) and the top left vertex point which is (-x,y)

the two "x" values are the same from 0 to x and from 0 to -x (distance is not negative)

the height of the rectangle is y but y=6-x^2

A=base*height

A=(2x)(6-x^2)

A=12x-2x^3

take the first derivative

A'=12-6x^2

set the first derivative to 0 and solve for x

12-6x^2=0

6x^2=12

x^2=2

x=√2

the base is 2√2

the height is 6-(√2)^2=6-2=4

base=2*1.4142=2.8284

base=2.83 units

height=4 units