when the deceleration of the wheel has a magnitude of 0.281 rev/s2 and the initial angular velocity is (a) +0.920 rev/s and (b) +2.24 rev/s.

Question

At a county fair there is a betting game that involves a spinning wheel. As the drawing shows, the wheel is set into rotational motion with the beginning of the angular section labeled "1" at the marker at the top of the wheel. The wheel then decelerates and eventually comes to a halt on one of the numbered sections. The wheel in the drawing is divided into twelve sections, each of which is an angle of 30°. Determine the numbered section on which the wheel comes to a halt when the deceleration of the wheel has a magnitude of 0.281 rev/s² and the initial angular velocity is (a) +0.920 rev/s and (b) +2.24 rev/s.

(a)	Numbered section =
(b)	Numbered section =

Answer 1

For the angular kinematics with constant angular acceleration you can use

Δθ=ω₀t+0.5αt^2 and ω=ω₀+αt

Here in your problem, α is negative since the wheel is decelerating.

For part a, then, we have following equations:

Δθ=0.920 t – (0.5) (0.281) t^2 and ω=0.920 – 0.281 t

Using the latter, you solve for the time it takes for the wheel to come to a halt. This is when ω=0, which gives you t=0.920/0.281=3.27 seconds. Inserting this value in the first equation, you get

Δθ= (0.920)(3.27) – (0.5)(0.281)(3.27)^2 = 1.506 revolutions = 1.506 rev x 360^o/(1 rev)= 542.16^o

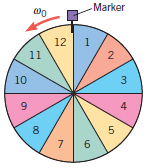
So, the net angular displacement becomes 542.16^o – 360^o = 182.16^o . And this corresponds to the 7th section. (182.16 / 30 = 6.072 > 6 ⇒ 7th section)

For part b, you do the exact same calculation using 2.24 rev/ sec instead of 0.920 rev / sec. I found Δθ=334.08^o (as the net displacement) and this corresponds to the 12th section. (334.08/30 = 11.136 > 11 ⇒12th section.)