Physic problem exercise

Question

The drawing shows a jet engine suspended beneath the wing of an airplane. The weight  of the engine is 9400 N and acts as shown in the drawing. In flight the engine produces a thrust  of 50100 N that is parallel to the ground. The rotational axis in the drawing is perpendicular to the plane of the paper. With respect to this axis, find the magnitude of the torque due to each of the following forces.

(a) the weight

_____ N · m

(b) the thrust

______ N · m

Answer 1

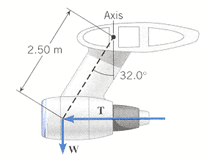
Using x-y coordinates as normal, Let e_r = unit vector in the radial direction and e_o = the unit vector in the angular direction. Let T = Thrust Force and W = Weight Force

Then the sum of the forces in the angular direction is Tsin(238^o) - Wcos(238^o)

= (50,100)(-.848) -(9,400)(-.53) = -37,506 e_o that is a total of 37,506 N in the ccw direction

But the angular (or torque) force from the Thrust = (50100)(-.848) = -42,487.2 N e_o

and the angular (or torque) force from the Weight = (-9,400)(-.53) = + 4,981.2 N e_o

Then the torque due to the weight is r x W = 2.5 e_r x 4,981.2 e_o = 12,453 N-m (the +k direction)

The torque due to the Thrust is 2.5 e_r x -42,487.2 e_o = -106,218 N-m (the-k direction)