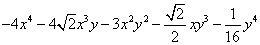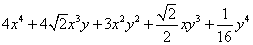Expand the following:

Question

 .

Answer 1

Without even doing this problem, you can see what the answer is given those choices. Because (√2x + 1/2y) has only positive numbers in it, when it is expanded by raising to the 4th power, all the terms MUST be positive, and there is only one answer with all positive coefficients.

To actually do the problem, you would just raise the first and last terms to the 4th power to get the first and last terms in the expansion so the first term is (√2x)⁴ = 4x⁴ and the last term is (1/2y)⁴ = 1/16y⁴.

To find the second, third, and 4th terms you would use the coefficients from Pascal's Triangle which are 1, 4, 6, 4, 1. The second term would use the second term in this row of Pascal's Triangle, 4. That 4 would be multiplied by the contribution from the first term cubed, (√2x)³ or 2√2x³, and the last term to the first power, (1/2y)¹ or just 1/2y. 4*2√2x³*1/2y = 4√2x³y

To find the third term, use the third coefficient from the row in Pascal's Triangle, 6, and multiply it by the first term squared (√2x)² or 2x² and by the last term squared (1/2y)² or 1/4y². 6*2x² *1/4y² = 3x²y²

To find the fourth term, use the fourth coefficient from the row in Pascal's Triangle, 4, and multiply it by the first term raised to the first power, (√2x)¹ or √2x, and the last term cubed (1/2y)³ = 1/8y³. 4*√2x*1/8y³ = 1/2√2xy³

Putting them all together you get: 4x⁴ + 4√2x³y + 3x²y² + 1/2√2xy³ + 1/16y⁴
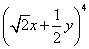