How to write an equation for a parabola in vertex form

Question

 Like if i was givin a graphed parabola how would i figure out how to write the equation, in vertex form/

Answer 1

The vertex form of a parabola's equation is generally expressed as : 

 

y=a(x−h)^2+k Where (h,k) is the max or min.

 

1.      Look at the graph.  

2.      Find the vertex of the graph (h,k)

3.      Vertex is the highest / lowest point of the graph known as Max or min  (h,K) 

 

Plug this into the form y=a(x−h)^2+k  Next solve for "a"

 

4.      To find the "a "  ----> pick a point on the graph other than vertex.  (usually y intercept)

5.       plug it into the vertex form and slove for "a"

 

 

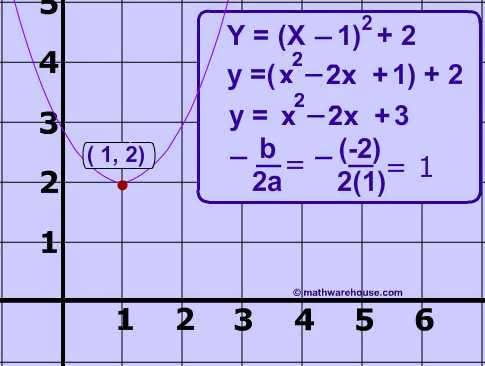
IF the general equation is given for the graph: y=ax^2+bx+c, then 

 

1.       to find the vertex: use formula x= -b/2a

2.       plug x into the given equation to find y value

3.       now you have (h,k)  

4.       find a point on the graph and plug in to the vertex form equation to find "a"

 

 

see below for example

y= x^2-2x+3 given: x= -b/2a ------> x= -(-2)/2(1)= 1-----> pug this into the given equation so y= 2

 

Min (1,2) and now pick x=0 so y=3 (0,3) to find "a"----->  in this case a = 1

y=a(x−h)^2+k    

y=(x−1)^2+2

 

 

Answer 2

Hi Aliyah,

I am in AZ too.

To write an equation for a parabola in vertex form, you need to read the coordinates of the vertex from the given graph as (h, k) first. You can write

y = a(x-h)^2 + k

Now, read the y-intercept or any other given point.

y-int = ah^2+k

You can solve for a,

a = (y-int-k)/h^2

So, the vertex form is y = [(y-int-k)/h^2](x-h)^2 + k

Answer 3

Some examples for the formula

 

The format of the equation that shows you where the vertex is

 

y = a(x - h)² + k

 

Example.  This parabola has a vertex at (3,4).

 

y = 2(x - 3)² + 4

 

Example 2.  This parabola has a vertex at  (1,1)

 

y = (x–1)² + 1

 

 

How to find "a"???

 

Pick a point on the graph other than the vertex.  Let's say you see the line pass through (1,5) and the vertex is at (3,4)...

 

 

First the vertex gives you this...

 

y = a (x - 3)² + 4

 

Put the values (1,5) into this equation.

 

 

5 = a (1 - 3)² + 4

 

Solve for a

 

5 = a*(-2)² + 4

5 = 4a + 4

1 = 4a

1/4 = a

 

Final equation is

 

y = 1/4*(x - 3)² + 4