Calculus question help please

Question

The tank shown is full of water.

(a) Find the work required to pump the water out of the spout. (Use 9.8 m/s² for g. Use 1000 kg/m³ as the weight density of water. Assume that a = 1.)

(b) Suppose that the pump breaks down after 4.7 × 10⁵

 J of work has been done. What is the depth of the water remaining in the tank? (Round your answer to the nearest tenth.)

Answer 1

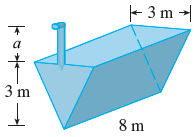
The first step is to compute the work against gravity performed on a thin layer of the liquid of width Δ y.

We place the center of our coordinate system in the vertex of the trough .It is easy to be seen that at a height y the cross section of the triangle has also length y

A thin layer at height y is a rectangular box of volume 8 y Δy and to lift it , we must exert a force against gravity equal to

Force on layer = g [ density] [ volume] ≈ 9.8 (1000 ) 8 y Δy

The layer has to be lifted a vertical distance of 4−y , so

Work on layer ≈ 78400 yΔy [ 4−y ]

Then W= ∫₀³ 78400 y [ 4−y ] d y =705600 Joules

THE SECOND PART OF THE PROBLEM

Here comes the tricky stuff.

The question being that after 4700000 Joules of work how many meters of water remain in the tank .

That is there is an amount of 705600 - 470000 = 235600 Joules of work to be done.

Let us say that the height of water is h

Then we need to solve the equation 9800 (8) ∫_y=0^y=h (4y-y²) d y = 235600 for h.

Or equivalently solve the equation ∫_y=0^y=h (4y-y²) d y = 3.0051

2y² - y³ /3 |₀^h = 3.0051

2h² - h³/3 = 3.0051

This equation requires a graphing calculator to be solved.

An easy way of doing this is to graph the function Y= 2x² - x³/3 - 3.0051 and choose the x intercept

that makes sense In our case x = 1.399953

Then the depth of the water remaining in the tank is h = 1.399953 meters

Answer 2

desmos.com/calculator/jfslpeytkf

Answer 3

a) The work/volume to lift water from a depth x (x is 0 at the top of the container and points downwards) will be ρg(x+a). The volume lifted will vary with x. The differential volume element is a rectangular box that is 8 by w(x) by dx. Note that we can express w(x) as 3 - 3(3/8 x) (It is a linear relation so that the width is 3 at x = 0 and 0 at x = 8)

The full expression for Work is The integral from x=0 to x=8 of (ρg(a+x)(8*3(1-3/8 x) dx

b) After a fixed number of Joules, how do you calculate depth of water left? (8-x)

Use same integral as in (a) but solve it from 0 to d and get an expression for W in terms of d. Solve numerically for the right d using Desmos or wolfram alpha. (You can rearrange the equation to be zero and find the zeroes. Note that the answer is 8-d