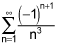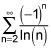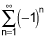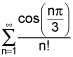Please help check my answer? Which of the following series converges conditionally?

Question

Which of the following series converges conditionally?

Diverges
Converges
Diverges
Converges Conditionally? I chose this

Answer 1

The first series converges. You can use the integral test on 1/n^3

The third series diverges. The sequence does not converge to 0.

The fourth series converges. The absolute value is bounded above by 1/n!, which has a ratio which converges to 0 (in fact, its sum is e).

Thus, let's look at the second function.

As we have (-1)^n, this is an alternating series.

As lim n -> ∞ ln(n) = ∞, lim n -> ∞ 1/ln(n) = 0

ln(n) < n, so 1/ln(n) > 1/n, whose sum diverges. (You can see this from the integral test, the integral of 1/n is ln(n) which again has a limit of ∞).

Thus, this series has conditional convergence.