Calculus graphs Double Prime, PLEASE HELP ASAP!

Question

Below is the graph of f '(x), the derivative of f(x), and has x-intercepts at x = -3, x = 1 and x = 2. There are horizontal tangents at x = -1.5 and x = 1.5. Which of the following statements is true?

 (4 po

Answer Choices:	f has an inflection point at x = -1.5.
	f is increasing on the interval from x = -3.2 to x = -4.5.
	f has a relative minimum at x = 1.5.
	All of these are true.

Answer 1

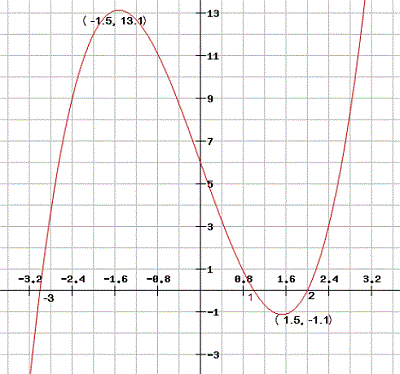
If f(x) had a relative min at x = -1.5, then f'(x) would change sign from negative to positive there. Since that is not the case, there is no relative min at x = -1.5.

When x < -3.2, f'(x) < 0. So, f is decreasing there.

To the left of x = -1.5, f'(x) is increasing, so (f')'(x) = f"(x) > 0. To the right of x = -1.5, f'(x) is decreasing, so f"(x) < 0. Since f"(x) changes sign when x = -1.5, the function y = f(x) has an inflection point at x = -1.5.