Tom K. answered • 08/01/20
Knowledgeable and Friendly Math and Statistics Tutor
Let's call the three listed integrals A, B, and C
Then,
a) the integral from 0 to 10 of f(x) is A + B = -2 + 14 = 12
b) As the integral from 3 to 8 of f(x) + C = B
the integral from 3 to 8 of f(x) equals B - C = 14 - 5 = 9
c) Let 1/3 x^2 + 5 = u
Then, du/dx = 2/3 x, or dx = 3/(2x) du
When x = 3, u = 1/3*3^2+5 = 3 + 5 = 8
When x = √15, 1/3x^2 + 5 = 1/3 * 15 + 5 = 10
Then, using I[a,b] for the integral from a to b.
I[3,√15] x f(1/3x^2 + 5) dx =
I[8, 10] x f(u) 3/(2x) du =
I[8, 10] 3/2 f(u) du =
3/2 I[8, 10] f(u) du =
3/2 C =
3/2 * 5 = 15/2 or 7 1/2


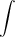 f(t)dt=-2
f(t)dt=-2

