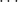Geometric series

Question

Determine whether the geometric series is convergent or divergent. If it is convergent, find its sum. (If the quantity diverges, enter DIVERGES.)

10 − 8 + 6.4 − 5.12 +  

Answer 1

A geometric series has the form: a + ar + ar² + ar³ + ...

where a is the first term and r is the multiplier (or common ratio). If this multiplier is between -1 and 1 (|r|<1), then the sum converges.

To find r, since we know this is a geometric series, we can simply divide the 2nd term (-8) by the 1st term (10), which gives us

r = -4/5

Because |r| is less than 1, we know this series converges. Using the formula S = a/(1-r), where S is the total sum of the series, and we know already a=10 and r=-4/5

S = 10/(1+4/5) = 50/9

Answer 2

r = -8/10 = - 0.8; IrI =0.8 < 1 converges

S = a₁/(1 - r) = 10/1.8 = 50/9