Does the function satisfy the hypotheses of the Mean Value Theorem on the given interval?

Question

A) Does the function satisfy the hypotheses of the Mean Value Theorem on the given interval?

f(x)=e^-3x , [0,2]

Choose the correct answer:

1. Yes, it does not matter if f is continuous or differentiable; every function satisfies the Mean Value Theorem.
2. No, f is not continuous on [0, 2].    
3. There is not enough information to verify if this function satisfies the Mean Value Theorem.
4. Yes, f is continuous and differentiable on 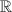, so it is continuous on [0, 2] and differentiable on (0, 2) .
5. No, f is continuous on [0, 2] but not differentiable on (0, 2).

If it satisfies the hypotheses, find all numbers c that satisfy the conclusion of the Mean Value Theorem. (Enter your answers as a comma-separated list. If it does not satisfy the hypotheses, enter DNE).

c=____

B) Let f(x)= (x-3)^-2. Find all the values of c in (2,5) such that f(5)-f(2)= f'(c)(5-2). (Enter your answers as a comma-separated list. If an answer does not exist, enter DNE.)

C= DNE

Based off of this information, what conclusions can be made about the Mean Value Theorem?

A. This contradicts the Mean Value Theorem since f satisfies the hypotheses on the given interval but there does not exist any c on (2, 5) such that f'(c)= f(5)-f(2)/5-2

B. This does not contradict the Mean Value Theorem since f is not continuous at x = 3.

C. This does not contradict the Mean Value Theorem since f is continuous on (2, 5), and there exists a c on (2, 5) such that f'(c)= f(5)-f(2)/5-2

D. This contradicts the Mean Value Theorem since there exists a c on (2, 5) such that f'(c)= f(5)-f(2)/5-2, but f is not continuous at x=3.

E. Nothing can be concluded.

Answer 1

A) f(x) = e⁻³ˣ, [0,2]

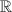Yes, f is continuous and differentiable on , so it is continuous on [0, 2] and differentiable on (0, 2).

[f(2) – f(0)]/(2 – 0) = (e⁻⁶ – 1)/2 and f'(x) = –3e⁻³ˣ

We can find the value of c that satisfies

f'(c) = [f(2) – f(0)]/(2 – 0) by writing

–3e⁻³ᶜ = (e⁻⁶ – 1)/2 and solving for c

c = –⅓ ln[(1 – e⁻⁶)/6] ≈ 0.598

B) Let f₂(x)= (x-3)⁻², (2,5).

Strictly following the way the question is presented,

c = DNE

There is no value of c in (2,5) such that f(5) – f(2)= f'(c)(5 – 2).

c = 5 satisfies f(5) – f(2)= f'(c)(5 – 2), but 5 is not in the open interval (2,5).

B. This does not contradict the Mean Value Theorem since f is not continuous at x = 3.

Answer 2

A) The MVT applies to any function continuous on the closed interval [a , b] and differentiable on the open interval (a , b). All exponential functions are both continuous and differentiable over  therefore the MVT applies to the given f(x). The MVT applied to f(x) on [0 , 2] guarantees an x-value, c, with 0 < c < 2, such that f^'(c) = [f(2) - f(0)] / (2 - 0) (ie the average rate of change of f on [0 , 2]).

Avg roc of f = (e^-6 - 1) / 2

f^'(x) = -3e^-3x

f^'(c) = -3e^-3c = (e^-6 - 1) / 2

e^-3c = (e^-6 - 1) / -6

-3c = ln [(e^-6 - 1) / -6] ~ -1.79

c ~ .598

B) Nothing in this example will contradict the MVT since f(x) is not continuous at x = 3, which is included in the closed interval [2 , 5]. Therefore, the MVT does not apply to f(x) on this interval.

[f(5) - f(2)] / (5 - 2) = [1/4 - 1] / 3 = -1/4

f^'(x) = -2 / (x - 3)³ = -1/4

(c - 3)³ = 8

c = 5 which is not in (2 , 5) but that is immaterial