
Bfsfsf G.
asked • 02/14/23For which positive integers k is the following series convergent? (Enter your answer as an inequality.)
| ∞ | (n!)2 |
| (kn)! | |
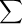 | |
| n = 1 |
1 Expert Answer

Aime F. answered • 02/17/23
Experienced University Professor of Mathematics & Data Science
It's not clear if you mean the summand to be (n!)²/(kn)! or its reciprocal.
For k = 1, (n!)²/(kn)! → ∞ as n → ∞ so that sum would diverge.
For k > 1, by the Ratio Test
r = (((n+1)!)²/(kn+k)!)/((n!)²/(kn)!)
= (n + 1)²/((kn+k)(kn+k–1)...(kn+1))
= (n + 1)²/nk((k+k/n)(k+(k–1)/n)...(k+1/n)).
For k > 2, clearly r → 0 as n → ∞, so the series converges.
For k = 2, r → 1/(2×2) = 1/4 < 1 as n → ∞, so the series converges.
Still looking for help? Get the right answer, fast.
Get a free answer to a quick problem.
Most questions answered within 4 hours.
OR
Choose an expert and meet online. No packages or subscriptions, pay only for the time you need.





Stanton D.
This question may have had a content initially, but Bfsfsf G., you have hashed it into nonsense. Please check your queries after you generate them, to avoid such an embarassment.02/14/23