(e) lim x → 0− h(x) 1 (f) lim x → 0+ h(x) 1 (g) lim x → 0 h(x) 1 (h) h(0) (i) lim x → 2 h(x) (j) h(2) (k) lim x → 5+ h(x) (l) lim x → 5− h(x)

Question

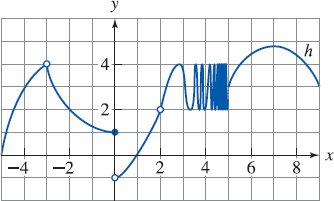The x y coordinate plane is given. The curve enters the window at the point (−5, 0), goes up and right to the open point (−3, 4), and goes down and right to the closed point (0, 1). The curve starts again at the open point (0, −1), goes up and right to the open point (2, 2), and then oscillates at an increasing rate between y = 2 and y = 4 until it reaches the x-value of 5. Between the x-values of 4.5 and 5 the oscillations are too close together to distinguish individual curves. At (5, 3) the oscillations stop and the curve goes up and right, changes direction at the approximate point (7, 4.8), goes down and right, and exits the window in the second quadrant.

(e)

lim x → 0⁻ h(x)

(f)

lim x → 0⁺ h(x)

(g)

lim x → 0 h(x)

(h)

h(0)

(i)

lim x → 2 h(x)

(j)

h(2)

(k)

lim x → 5⁺ h(x)

(l)

lim x → 5⁻ h(x)

Answer 1