Raymond B. answered • 04/12/22
Math, microeconomics or criminal justice
at first it appears the answer you want is 40-25sqr5 Just switch the signs.
that assumes 25sqr5 -40 is correct as the integral of 15xsqr(x^2+4)
That is the solution SnapXam, an online integral calculator has
integration tables on wikipedia also have the same integral
for sqr(x+a) =(1/3)(x^2+a)^(3/2)
when a =4, and multiply by 15 you get the same answer
check the integral by taking the derivative and see if it is 15xsqr(x^2+4)
[5(x^2+4)^(3/2)]'
= (3/2)(5)(x^2+4)^(1/2)(2x
= 15x(x^2+4)^(1/2)
evalute the integral between 0 and 1
5(0^2 +4)^(3/2) - 5(1^2 +4)^(3/2
=5[4^(3/2) - 5^(3/2)]
=5(8 -5sqr5)
= 40 -25sqr5 which is just switching the signs of 25sq5-40
you probably have a typo when you typed 15x(sqr x^2)+4 dx
but if you somehow really meant that then
the integral of 15x(sqrx^2)+4 dx
= the integral of 15x(x) +4 dx
= 5x +4t
evaluated from 0 to 1 is 9
evaluated from 1 to 0 is -9, Again just change the sign


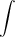
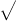 x
x


Kelly B.
Yes, I had a typo with 15x(sqrt x^2)+4, it was meant to be 15x(sqrt x^2+4)..04/12/22