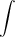Calculus Question

Question

Let g(x) = x	f(t) dt
0

,

 where f is the function whose graph is shown.

(a) Evaluate g(0), g(3), g(6), g(9), and g(18).

g(0)	=
g(3)	=
g(6)	=
g(9)	=
g(18)	=

(b) On what interval is g increasing? (Enter your answer using interval notation.)

 

(c) Where does g have a maximum value?

x = 

(d) Sketch a rough graph of g.

Answer 1

(a)

1. g(0) is the integral from 0 to 0 of f(t) with respect to t, so g(0) = 0.
2. g(3) is the integral from 0 to 3 of f(t) with respect to t, so this is the area between the graph of f(t) and the t-axis on the t-interval (0, 3), which is the area of a rectangle with height 6 and width 3, so g(3) = 18.
3. g(6) is the integral from 0 to 6 of f(t) with respect to t, so this is the area between the graph of f(t) and the t-axis on the t-interval (0, 6), which is the the previous area plus the area of a copy of that rectangle and half of that rectangle, so g(6) = 18 + 18 + 9 = 45.
4. g(9) is the integral from 0 to 9 of f(t) with respect to t, so this is the area between the graph of f(t) and the t-axis on the t-interval (0, 9), which is the the previous area plus the area of half of a 12x3 rectangle, so g(6) = 45 + 18 = 63.
5. g(18) is the integral from 0 to 18 of f(t) with respect to t, so this is the area between the graph of f(t) and the t-axis on the t-interval (0, 18), which is the the previous area MINUS the area of the polygon under the t-axis on the t-interval (9, 18), which consists of half of a 6x6 rectangle and a 6x3 rectangle, so g(18) = 63 - (18 + 18) = 27.

(b) g is increasing from x=0 to x=9 since g increases from g(0)=0 to g(9)=63, so g is increasing on the interval (0, 9).

(c) g has a maximum value at x=9 because g increases from 0 to 63 (see part b) but then decreases from there since we subtract the area under the t-axis.

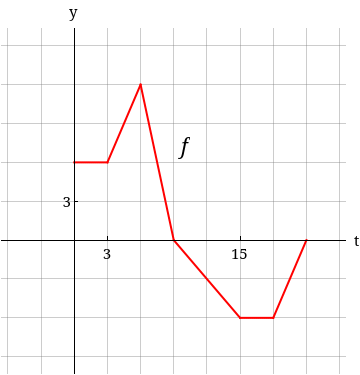
(d) Based on the answers in parts a-c, the graph of g is the top-left graph.