Calculus Question

Question

The table gives the values of a function obtained from an experiment. Use them to estimate 9	f(x) dx
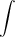3

 using three equal subintervals with right endpoints, left endpoints, and midpoints.

x	3	4	5	6	7	8	9
f(x)	−3.6	−2.1	−0.7	0.2	0.8	1.3	1.7
(a) Estimate 9	f(x) dx
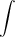3

 using three equal subintervals with right endpoints.

R₃ =  _____

If the function is known to be an increasing function, can you say whether your estimate is less than or greater than the exact value of the integral?

(b) Estimate 9	f(x) dx
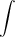3

 using three equal subintervals with left endpoints.

L₃ =  _____

(c) Estimate 9	f(x) dx
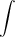3

 using three equal subintervals with midpoints.

M₃ =  _______

Answer 1

For the right endpoints, we can choose f(5), f(7), and f(9) and each interval has a width of 2. So our estimate is:

2 * ( f(5) + f(7) + f(9) ) = 2 * ( -0.7 + 0.8 + 1.7 ) = 3.6

For the left endpoints, we can choose f(3), f(5), and f(7). Similarly, for the midpoints, we can choose f(4), f(6), and f(8). Can you figure out the estimates using the left endpoints and midpoints from what we have so far?