Calculus Question

Question

Sketch the graph of f by hand and use your sketch to find the absolute and local maximum and minimum values of f. (If an answer does not exist, enter DNE.)

f(x) =	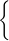49 − x2		if −7 ≤ x < 0
2x − 2	if 0 ≤ x ≤ 7
absolute maximum
absolute minimum
local maximum
local minimum

Answer 1

f(x) = 49-x^2 is a downward opening parabola with vertex = maximum point = (0, 49)

49 is the absolute and local maximum

the absolute minimum is when x=-7 in the interval [-7,0]

f(0) = 49-0^2 = 49= max

f(-7) = 49-(-7)^2 = 49-49-0 = the absolute minimum of the interval [-7,0]

f'(x) = -2x -2

has an absolute minimum at x=7, f(7)= -14-2 = -16

f(0) = -2 would be the absolute maximum but 0 is not in the interval, so the absolute maximum does not exist DNE

the graph is a straight line with one endpoint as the absolute minimum

with no local max or min in between

However, the way the boxes are listed, it isn't fully clear what interval is intended to go with which function.