A winch at the top of a 12-meter building pulls a pipe of the same length to a vertical position, as shown in the figure.

Question

The winch pulls in rope at a rate of −0.1meter per second (ds/dt = −0.1 m/sec).

Find the rate of vertical change and the rate of horizontal change at the end of the pipe when y = 4. (Round your answers to three decimal places.)

horizontal ?m/sec

vertical ?m/sec

Answer 1

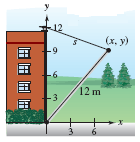
Let

h = 12 m be the height of the building and the length of the pipe,

s(t) be the length of the rope at time t,

x(t) be the x position of the pipe's end at time t,

y(t) be the y position of the pipe's end at time t,

s'(t) = -0.1 m/s be the rate of change of s(t),

x'(t) be the rate of change of x(t),

y'(t) be the rate of change of y(t),

t₁ be the time value at which y(t₁) = 4m.

We are to calculate x'(t₁) and y'(t₁).

For simplicity abbreviate

s = s(t)

x = x(t)

y = y(t)

s' = s'(t) = -0.1 m/s

x' = x'(t)

y' = y'(t)

s₁ = s(t₁)

x₁ = x(t₁)

y₁ = y(t₁) = 4 m

s₁' = s'(t₁) = -0.1 m/s

x₁' = x'(t₁)

y₁' = y'(t₁)

Apply the Pythagorean theorem to the right angle triangle whose hypotenuse is

the pipe, and whose one side is along the ground:

h² = x² + y²

So

x² = h² - y² (1)

Apply the Pythagorean theorem to the right angle triangle whose hypotenuse is

the rope, and whose one side is along the building:

s² = x² + (h-y)² (2)

Substituting (1) into (2)

s² = h² - y² + (h-y)²

= 2h² - 2hy (3)

From (3) express y

y = h - s²/2h

Calculate the derivative of y

y' = -ss'/h (4)

From (1) express

x = √(h² - y²)

Calculate the derivative of x

x' = (1/2) (-2yy')/√(h² - y²)

= -yy'/√(h² - y²) (5)

Now we can calculate the quantities at time t_1, given that we know y₁ and s₁'.

First calculate s₁ from equation (3)

s₁² = 2h² - 2hy₁

s₁ = √(2h² - 2hy₁) (6)

To calculate y₁', substitute s = s₁ from equation (6) into (4)

y₁' = -s₁s₁'/h = -s₁'√(2h² - 2hy₁)/h = -s₁'√(2(1 - y₁/h)) (7)

Substituting actual numbers

y₁' = -(-0.1)√(2×(1 - 4/12)) = 0.2/√3 = 0.11547 m/s

To calculate x₁' use equation (5)

x₁' = -y₁y₁'/√(h² - y₁²)

Substitute actual numbers

x₁' = -4×(0.2/√3)/√(12² - 4²) = -0.8/√(3×192) = -0.8/24 = -0.033333 m/s