Find the rate of vertical change and the rate of horizontal change at the end of the pipe when y = 4.

Question

A winch at the top of a 12-meter building pulls a pipe of the same length to a vertical position, as shown in the figure. The winch pulls in rope at a rate of −0.1 meter per second (ds/dt = −0.1 m/sec).

horizontal ?m/sec

vertical ?m/sec

Answer 1

x² + y² = 144; (12 - y)² + x² = s². I f y = 4 m, then x² = 144 - 16 = 128; x = √128 = 8√2 m

s² = 128 + 64 = 192; s = √192 = 8√3 m

(12 - y)² + 144 - y² = s²; 144 - 24y + y² + 144 - y² = s²; 288 - 24y = s²; - 24dy/dt = 2sds/dt;

dy/dt = - sds/t/12 = - 8√3(- 0.1)/12 = 0.11547 m/sec

2xdx/dt + 2ydy/dt = 0; dx/dt = - (y/x)dy/dt = -(8√3/8√2)·0.11547 m/sec = - 0.14142 m/sec

Answer 2

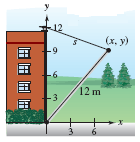
There are two right triangles in this problem, we can label the length of the sides and apply pythagoras' theorem to obtain the two equations we need to solve the problem.

xxxx

│ xxxxx S

│ xxxx

12-y │ xxxx

│ xxxx

│ xxxxx

└────────────────────x

x

┌────────────────────x

│ xxx

│ xxx

│ xxx

│ xx

│ xxx

y │ xx

│ xx

│ xxx 12

│ xx

│ xx

│ xxx

│ xx

│xxx

xx

The first triangle in green is with the base of the building, the point (x, y), and the point (x) distance on the ground. We know the hypotenuse is 12 m. Using Pythagoras' Theorem

x² + y² = 12²

The second right triangle in blue is made with the point on the roof building, the point (x, y), and the distance (x) of that point away from the building. The hypotenuse has side s, the base of the triangle is x, and the height of the triangle is 12 - y. Again using Pythagoras' Theorem

x² + (12 - y)² = s²

Given y = 4, we can find x, and then s. Through implicit differentiation of both equations we can then find dx/dt and dy/dt

In implicit differentiation, we apply the derivative on all variables in an equation. I will walk through applying implicit differentiation on the first equation. First we take the derivative of both sides with respect to time (d/dt)

(d/dt) (x² + y²) = (d/dt) 12²

The derivative of a number is a constant, so the right hand side is zero

(d/dt) (x² + y²) = 0

On the left hand side, we have an addition, so the rules of differentation have us apply the derivative on both parts, we currently have

(d/dt) x² + (d/dt) y² = 0

The derivative of x² is 2x, however don't forget that x is also changing with time. We must apply the chain rule and multiply by the derivative of x, we write this as (dx/dt).

(d/dt) x² = 2x * (dx/dt)

The same applies to the second term of (d/dt) y², so the implicit differentiation gives us,

2x * (dx/dt) + 2y * (dy/dt) = 0

And after simplifying

(dx/dt) = - (dy/dt)

This is the first equation we need.

To get the second, apply implicit differentiation on the pythagoras' theorem from the second triangle,

x² + (12 - y)² = s²

Working through the differentation (try it!) the answer is

2x (dx/dt) + 2 (12 - y) (-1) (dy/dt) = 2s * (ds/dt)

Or, dividing out the factor of 2,

x (dx/dt) - (12 - y) (dy/dt) = s * (ds/dt)

We now have two equations,

(dx/dt) = - (dy/dt)

x (dx/dt) - (12 - y) (dy/dt) = s * (ds/dt)

The horizontal change of the point is (dx/dt), and the vertical is (dy/dt). Now all that's left is to plug in the given value of (ds/dt) = -0.1, and y = 4.

You will need the values of x and s as well, but you can use the original two Pythagoras' equations to find them,

x² + y² = 12²

x² + (12 - y)² = s²