Answer the following question.

Question

A winch at the top of a 12-meter building pulls a pipe of the same length to a vertical position, as shown in the figure. The winch pulls in rope at a rate of −0.4 meter per second (ds/dt = -0.4 m/sec). Find the rate of vertical change at the end of the pipe when y = 1.

Answer 1

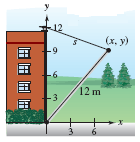
We can draw a perpendicular from the side of the building to the top end of the pipe at (x,y) which creates two right triangles. The bottom right triangle will give us an equation relating dx/dt and dy/dt, while the top triangle gives us an equation relating dx/dt, dy/dt, and dz/dt (where z is the hypotenuse of the top triangle, the distance from the top of the building to the top of the pipe), where dz/dt is known:

Also, at the instant y = 1, x = √143 , and z = √264 (all from pythag thm)

From bottom triangle: x² + y² = 144

2x·dx/dt + 2y·dy/dt = 0

dx/dt = - 1/√143 · dy/dt

From top triangle:

x² + (12 - y)² = z²

x² + y² - 24y + 144 = z²

2x·dx/dt + 2y·dy/dt - 24·dy/dt = 2z·dz/dt

√143·dx/dt - 11·dy/dt = √264·(-.4)

Substituting the expression for dx/dt from above yields ·-12dy/dt = √264·(-.4)

dy/dt = √264·(.4) / 12

Answer 2

(y + 12)²/4 + x²/4 + s²/4 = 144; and x² + y² = 144

(y + 12)² + 144 - y² + s² = 576; 24y = 288 - s²; 24dy/dt = - 2sds/dt; dy/dt = - sds/dt/12

If y = 1m then s = (288 - 24)^1/2 = 264^1/2 = 16.248 m

ds/dt = - 16.248·(- 0.4)/12 = 0.5416 m/s