
Kaitlyn M.
asked • 02/07/22Find k such that the line is tangent to the graph of the function. Function Line f(x) = k x y = 2x + 18 k =
Find k such that the line is tangent to the graph of the function.
| Function | Line |
f(x) = k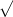
|
x |
| y = 2x + 18 |
k =
1 Expert Answer

Doug C. answered • 02/09/22
Math Tutor with Reputation to make difficult concepts understandable
Let the point on the graph of f be represented by (x, k√x). The given line passes through the point (0,18) with a slope of 2.
You can come up with two equations for the slope. One using the two points and another using the fact that the derivative of f(x) at the point where y = 2x+18 is tangent will also have a slope of 2.
So,
(k√x-18)/(x-0) = 2 (slope calculated using the two points.
1/2 (k) /√x = 2 (the derivative also equals 2)=> k = 4√x. Substitute that value into the 1st equation and solve for x. That will be the x -coordinate of the POT (point of tangency). Substitute that value into either equation to find the required value for k.
Still looking for help? Get the right answer, fast.
Get a free answer to a quick problem.
Most questions answered within 4 hours.
OR
Choose an expert and meet online. No packages or subscriptions, pay only for the time you need.





Mark M.
Review your post for accuracy. The table makes the data ambiguous.02/08/22